円錐 体積 求め 方 123563-円錐 体積 公式 求め 方

体積（立方センチメートル）を $1000$ で割ればリットルに変換できます。 例題1 一辺の長さが $\\mathrm{cm}$ である立方体の容器に水を満タンに入れた。体積（立方センチメートル）を $1000$ で割ればリットルに変換できます。 例題1 一辺の長さが $\\mathrm{cm}$ である立方体の容器に水を満タンに入れた。角錐や円錐の体積の公式はこれと似ています。同じように、底面積と高さを掛けます。その後、 3分の1にすることで体積が出ます。 つまり、角錐と円錐の体積を出す公式は以下のようになります。 角錐・円錐の体積 = 底面積 × 高さ × $\displaystyle\frac{1}{3}$

中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ

円錐 体積 公式 求め 方

円錐 体積 公式 求め 方-円錐の関連記事はこちら 中学数学円錐の体積の求め方・公式サクッと 中学数学円錐の高さの求め方頻出パターン 中学数学円錐の中心角の求め方3パターン立体の体積の求め方 これで，円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが，以上の議論は，「任意の立体について，基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば，その立体の体積を定積分により求めることができる。

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積＝15m 3 、半径＝2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定し円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積＝15m 3 、半径＝2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定しどちらの方法でも、確かに円錐の体積は \(\color{red}{V = \displaystyle \frac{1}{3}\pi r^2 h}\) と求められました。 このように、ある立体の体積は その立体をなす平面の面積の積み重ね（または回転）で求められる のですね。

回転体の体積の求め方 作成者 Bunryu Kamimura トピック 回転体三角形 扇形の回転体 球欠＋円錐の体積円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。 このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。円錐台の体積の求め方 円錐台の体積の求め方についての質問です。 上底の半径=3 下底の半径=4 高さ=3 円周率=π この場合、大きな円錐の体積－小さな円錐の体積 という考え方や円錐 台の公式がある(

円錐の体積の公式を用いた場合 円錐の体積の公式より， V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より， ∫ a b f (x) d x = F (x) a b = F (b) − F (a) （ F (x) は f (x) の原始関数の1である ） 求める円錐の底面積 S (x) を S (x) = π {f③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形，高さが の四角錐を考える． これを6つ組み合わせる． この立方体の体積＝ 1つの四角錐の体積は次式で表される． 四角錐の体積＝ →「底面積×でしたら、今からお教えする解き方を きちんとマスターしておきましょう！ まずは公式です。 これは必須事項ですので 必ず！ 覚えるようにしてください。 円錐の体積 ＝（底面積）×（高さ）× 1/3 では、この公式を実際に 当てはめてみましょう！

無料ダウンロード 円錐 体積 求め 方 壁紙 配布

円錐の体積を求める Youtube

例 3 65 (円錐の体積) 底面の半径 ，高さ の円錐の体積は である． これを多重積分で求める． 円錐の底面は 平面にあるとし， その領域を相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね！ それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの円錐の体積の公式を用いた場合 円錐の体積の公式より， V = 1 3 π r 2 h = 1 3 π × 1 2 × 1 = π 3 定積分の公式を用いた場合 定積分の基本式より， ∫ a b f (x) d x = F (x) a b = F (b) − F (a) （ F (x) は f (x) の原始関数の1である ） 求める円錐の底面積 S (x) を S (x) = π {f

体積の求め方 計算公式一覧

一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋

回転体の体積の求め方 作成者 Bunryu Kamimura トピック 回転体三角形 扇形の回転体 球欠＋円錐の体積③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形，高さが の四角錐を考える． これを6つ組み合わせる． この立方体の体積＝ 1つの四角錐の体積は次式で表される． 四角錐の体積＝ →「底面積×円錐台の体積の求め方 円錐台の体積の求め方についての質問です。 上底の半径=3 下底の半径=4 高さ=3 円周率=π この場合、大きな円錐の体積－小さな円錐の体積 という考え方や円錐 台の公式がある(

体積の求め方 計算公式一覧

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

円錐の体積＝底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク 円錐の体積を求める問題 // では、実際に円錐の体積を求める問題を解いていきたいと思います。図の円すいの体積を求めなさい。 問題の見方 立体の体積を求める公式より，～～すいとつく立体の場合， $$(底面積)×(高さ)×\frac{1}{3}=(体積)$$ で求められます。～～すいの立体のときは，$$\frac{1}{3}$$をかけ算するのがポイントです。7 立体の体積と表面積 143 右の図の円錐について，次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。

円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題

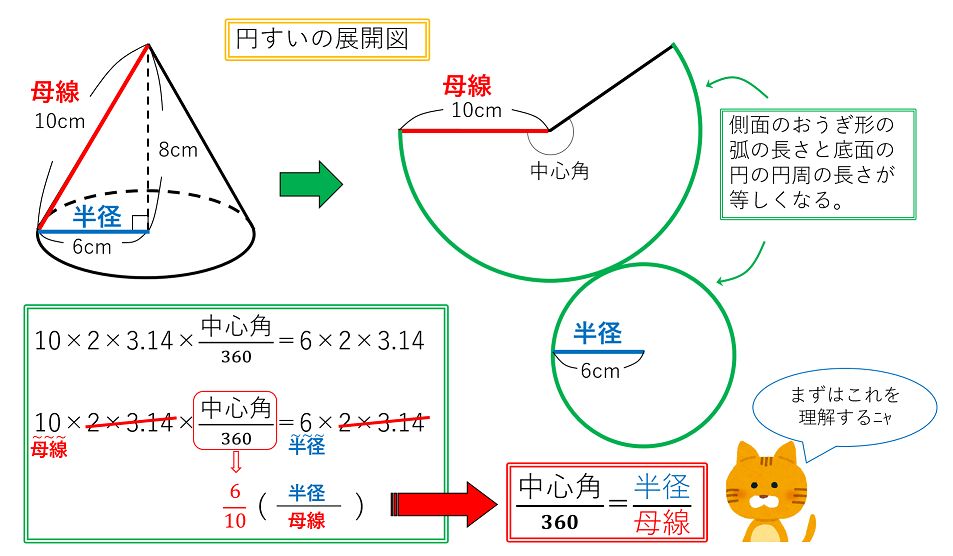
公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ

どちらの方法でも、確かに円錐の体積は \(\color{red}{V = \displaystyle \frac{1}{3}\pi r^2 h}\) と求められました。 このように、ある立体の体積は その立体をなす平面の面積の積み重ね（または回転）で求められる のですね。次の章では、学校で学習する円錐の基本的な考え方について解説していくよ！ 簡単なやり方だけでなく、基本的な考え方も身につけておけると数学の基礎力向上にもつながってきます。 がんばって理解していきましょう♪ スポンサーリンク底面積を求めて $$\pi \times 3^2=9\pi$$ 体積の公式に当てはめて $$9\pi \times 4 \times \frac{1}{3}$$ $$=12\pi cm^3$$ となります。 半径がわからない場合でも 考え方は、高さを求めるときと同じですね！ 円錐の体積を求める方法 まとめ お疲れ様でした！ 円錐の体積を

三角錐の体積の求め方 Geogebra

三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ

あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。 半球の体積＝（a＋4×3／4a）／6×h＝（2／3）・ah 円錐×2＝半球 円錐×3＝円柱 ということですか。円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐の体積の求め方を教えてください 底面の直径と母線の長さがともに8c Yahoo 知恵袋

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

円錐の体積の求め方 公式 小学生 中学生の勉強

円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋

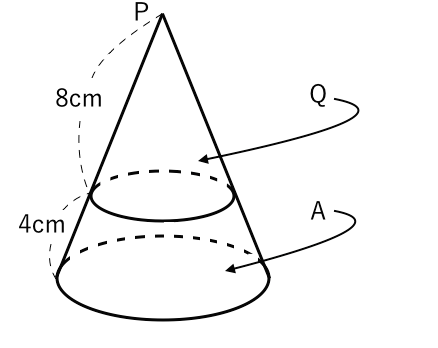
高さの分からない円すい展開図 どうやって立体の体積を求めるの

円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく

円錐 体積の比較 中学から数学だいすき

中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ

裏技 プリン型の立体の体積 一瞬で求められますか Youtube

体積の求め方 計算公式一覧

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

高さの分からない円すい展開図 どうやって立体の体積を求めるの

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

相似比と体積の計算 円錐台 三角錐台 中学３年数学 Youtube

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

相似な図形 体積比 相似な図形に注目せよ 苦手な数学を簡単に

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

球の表面積と体積の公式 数学fun

円錐の体積ってなんであの公式なの Webty Staff Blog

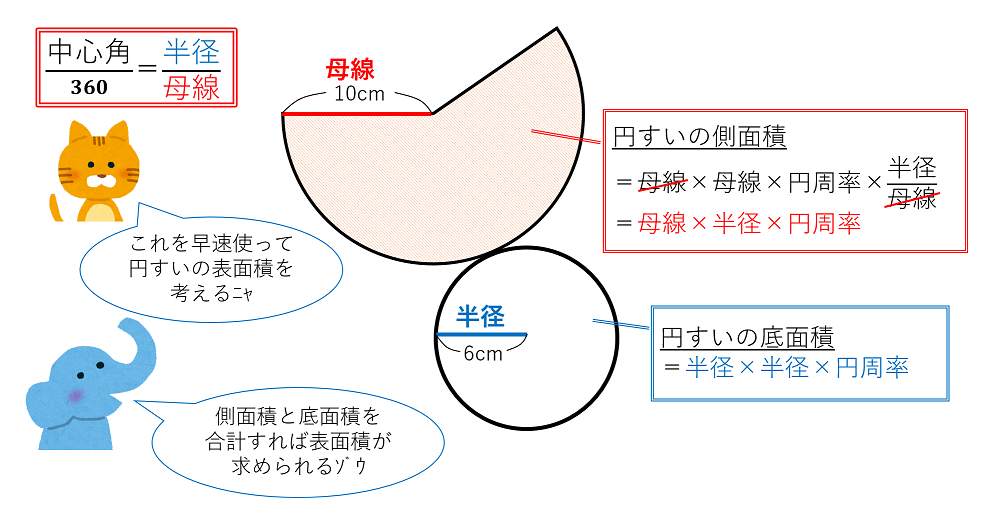
公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学

角錐と円錐の体積 Youtube

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室

円錐の表面積 Youtube

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun

体積の求め方 計算公式一覧

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

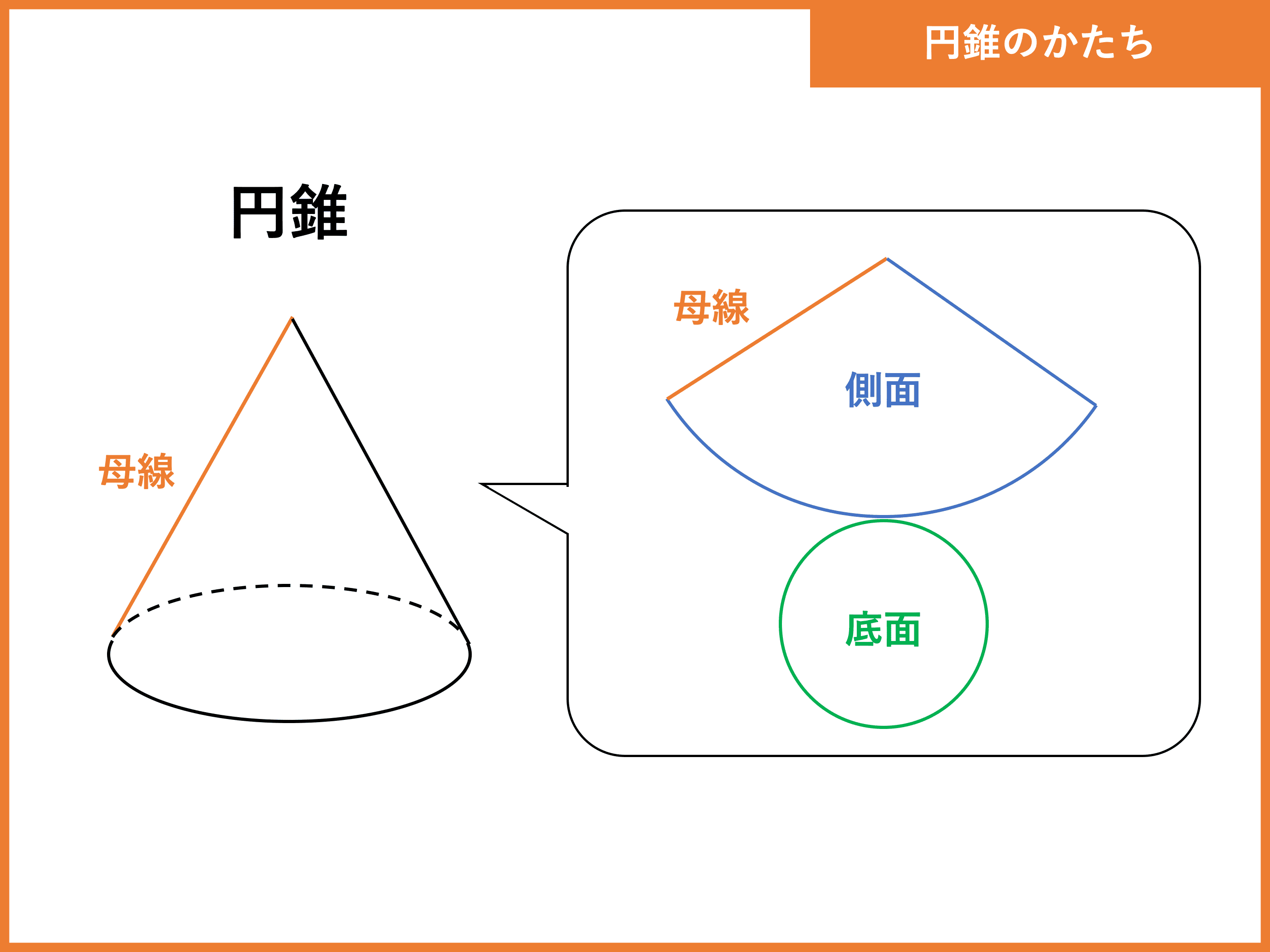
円錐とは 体積 表面積の公式や求め方 受験辞典

体積の求め方 計算公式一覧

円錐の体積の求め方 公式と計算例

高さの分からない円すい展開図 どうやって立体の体積を求めるの

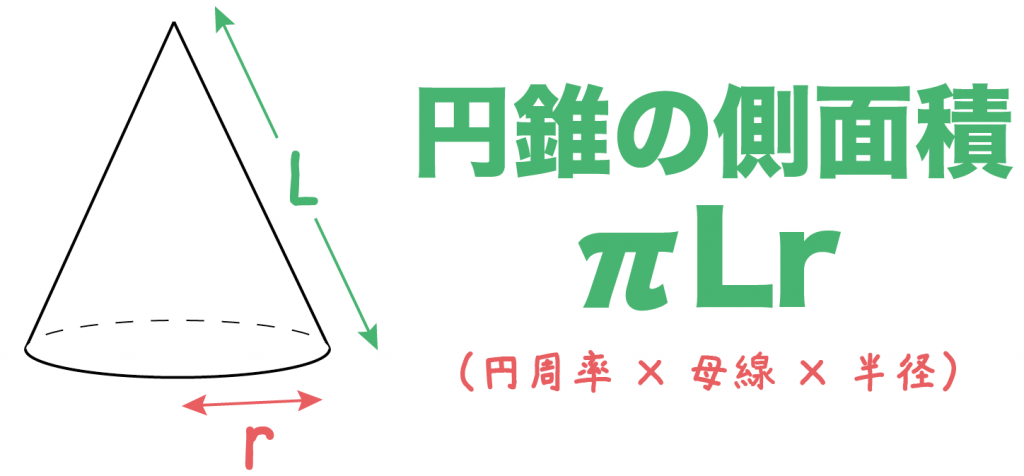
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

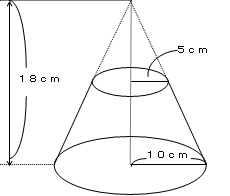
体積 円錐台の体積を求める 子供に教える算数のツボ

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

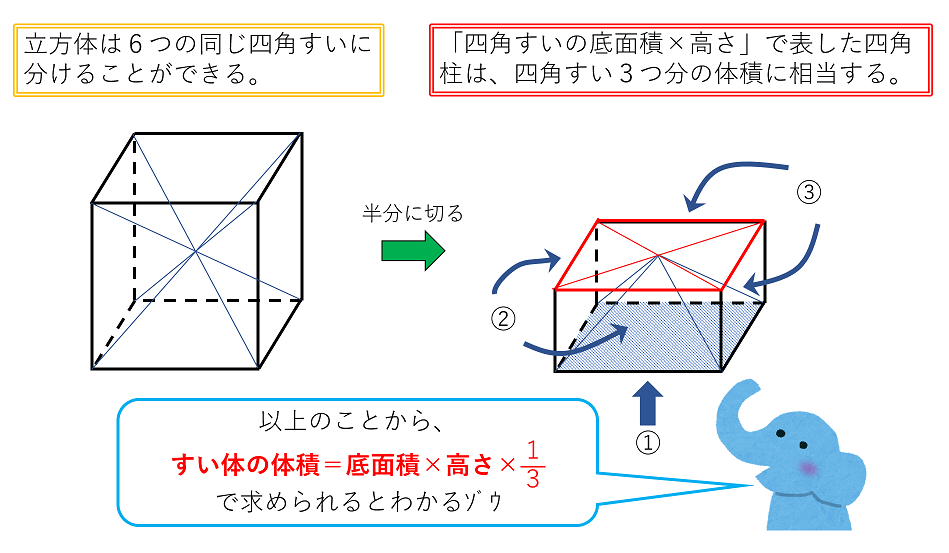
公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

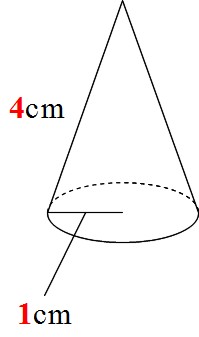
Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ

角錐 円錐の体積と表面積の公式 数学fun

三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

円すいの高さの求め方を教えて下さい できたらr でお願いします ど Yahoo 知恵袋

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

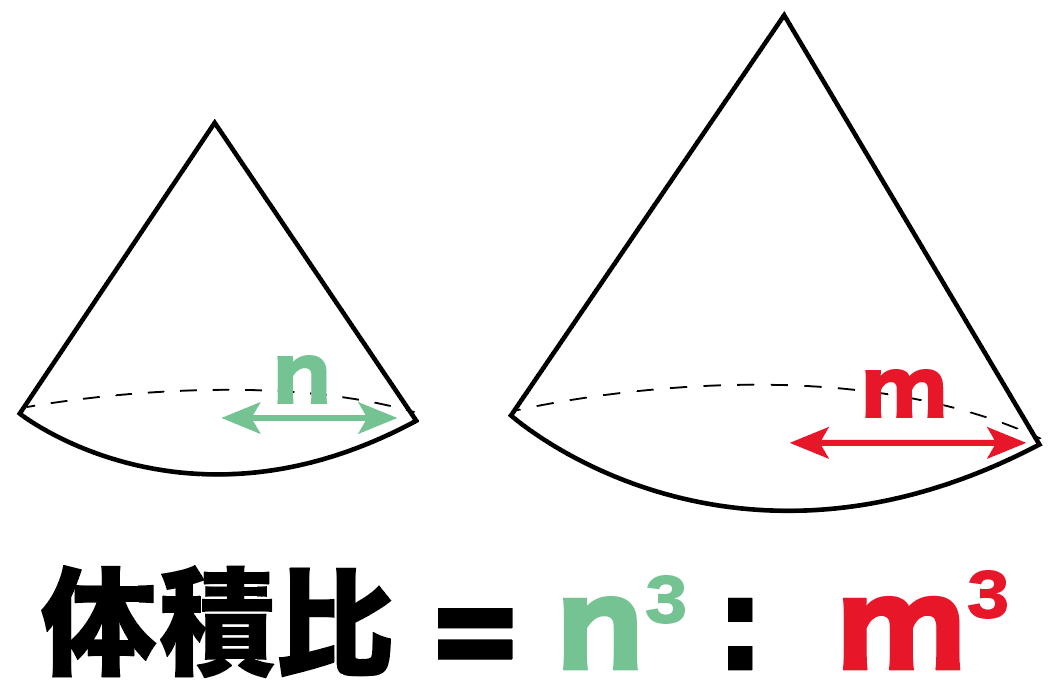
3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく

高さの分からない円すい展開図 どうやって立体の体積を求めるの

中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット

中3 三角形の相似 円錐の体積比 日本語版 Youtube

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明

円錐の表面積の求め方 公式と計算例

高さの分からない円すい展開図 どうやって立体の体積を求めるの

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

高さの分からない円すい展開図 どうやって立体の体積を求めるの

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

空間図形14 円すい台の体積 Youtube

図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋

円すい 円錐 の体積の求め方と問題 小学数学 Irohabook

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

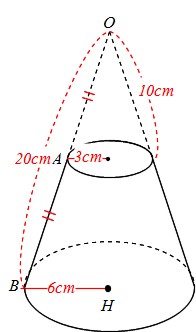
Math 円錐 円錐台と面積比 体積比 働きアリ

円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

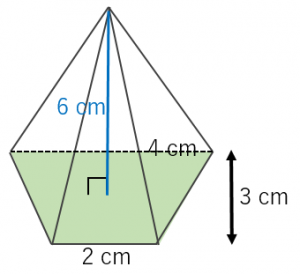
三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

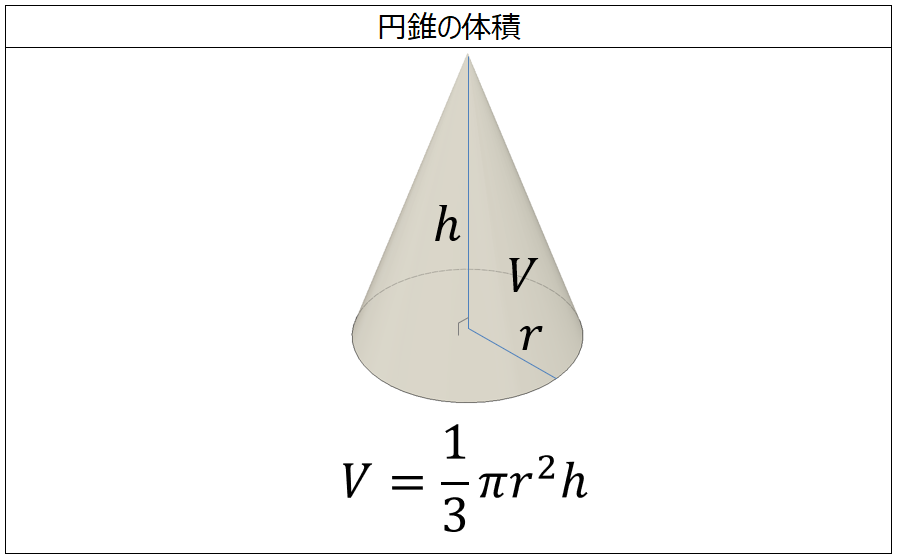
体積の計算 円錐 製品設計知識

角錐 円錐の体積 Youtube

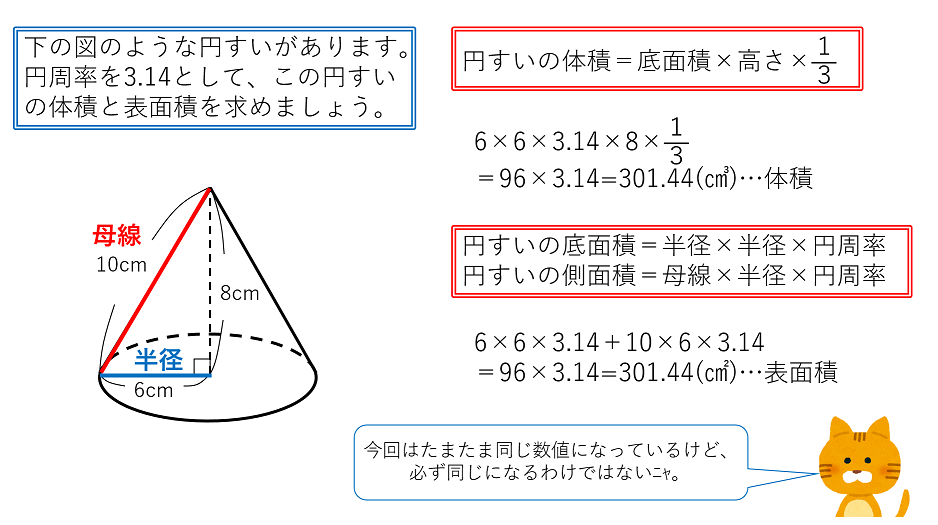
公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ

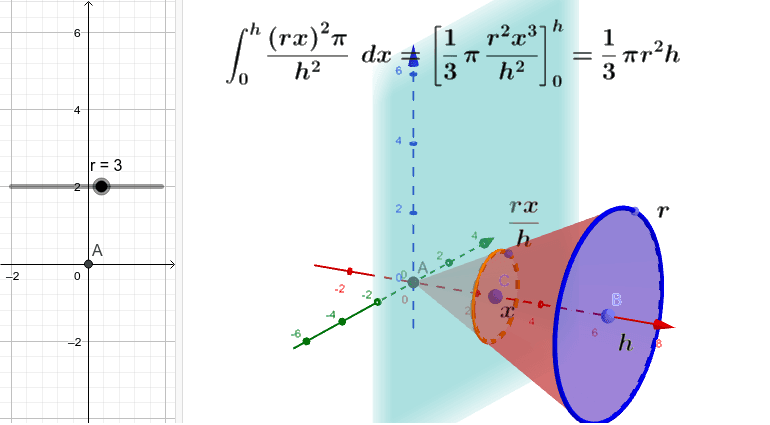
円錐の体積の求め方 Geogebra

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

Incoming Term: 円錐 体積 公式 求め 方, 円錐 体積 の 求め 方,